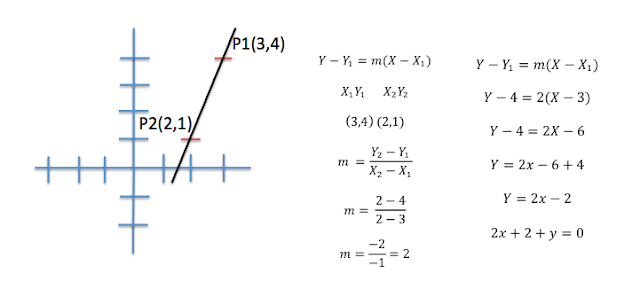Donde se encontraran con videos explicativos,ejercicios de muestra y ejercicios para poner en practica.''
1.LINEA RECTA Es la distancia mas corta entre dos puntos,lo que quiere decir que es DISTANCIA,lo que en geometría analítica se define como el segmento dado por dos puntos, P1(x1,y1) y P2 (x2,y2).

V I D E O S E X P L I C A T I V O S
¿Cómo hallar una distancia entre dos puntos? (d)
Pendiente de una recta (m)
Ecuación de la recta de la forma punto-pendiente
E J E M P L O S
1.Hallar a distancia entre P1(-3,1) y P2(4,2)
2.Hallar la pendiente (m) de una recta que pasa por los puntos P1(-1,3) y P2(2,-2)
3.Halla la ecuación de una recta que pasa por los puntos P1(3,4) y P2(2,1)
4.Hallar la ecuación de una recta que pasa por los puntos (0,-3) (4,0) y que pase por el punto (0,2)
5. Dos rectas perpendiculares se interceptan en el punto (4,4),si uno de ellos pasa por el origen,halla la ecuación de las 2 rectas.
E J E R C I C I O S D E P R A C T I C A
1.Halla la distancia de una recta que pasa por los puntos (4,2) y (3,4).
2.Halla la pendiente de una recta que pasa por los puntos (-1,-4) y (-3,-2)
3.Halla la ecuación de una recta que pasa por los puntos (-3,6) y (3,3)
4.Halla la pendiente de una recta que pasa (-1,2) y (-4,-6)
5.Halla la ecuación de una recta que pasa por los puntos (9,2) y (1,4)
2.CIRCUNFERECIA Y ELIPSE
CIRCUNFERENCIA: Es el conjunto de todos los puntos de un plano que equidistan (igual distancia entre dos puntos) de otro punto fijo.
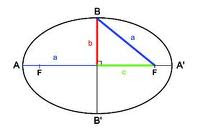
ELIPSE:Lugar geometrico de todos los puntos de un plano,tales que su suma de las distancias de dos puntos fijos llamados focos sea una constante.
V I D E O S E X P L I C A T I V O S
¿Cómo hallar la ecuación de la circunferencia con centro en el origen?
¿Cómo hallar la ecuación de la circunferencia cuando el centro no es el origen ?
¿Cómo hallar la ecuación de los focos y coordenadas de la elipse?
E J E M P L O S
1.Escribir la forma canonica de la ecuación de la circunferencia con centro en el origen y radio 6.
2.Escribir la forma canonica de la ecuación de la circunferencia con centro en (2,3) y radio 4.
3.Encuentra la distancia entre los puntos (-2,-3) y (3,4) de la circunferencia.
4.Halla los focos de la siguiente elipse
E J E R C I C I O S D E P R A C T I C A
1.Escribir la forma canonica de la circunferencia con centro en el origen y radio en 5.
2.Escribir la forma canonica de la ecuación de la circunferencia con centro en (5,3) y radio 6.
3.Encuentra la distancia entre los puntos (-1,-5) y (2,7) de la circunferencia.
4.Dada la ecuación reducida de la elipse  , hallar las coordenadas de los vértices de los focos.
, hallar las coordenadas de los vértices de los focos.
5.Hallar la ecuación de la elipse de foco F(7, 2), de vértice A(9, 2) y de centro C(4, 2).
3.PARABOLA E HIPERBOLE
PARABOLA:Se define como el lugar geométrico de los puntos de un plano que equidistan de una recta (eje o directriz) y un punto fijo llamado foco.
HIPERBOLE:Es el lugar geométrico de los puntos de un plano tales que el valor absoluto de la diferencia de sus distancias a dos puntos fijos, llamados focos, es igual a la distancia entre los vértices, la cual es una constante positiva.
E J E M P L O S
1.Halla los vertices,los focos y las directrices de una parábola con ecuación:
y^2 - 4y - 6y + 9 = 0
2.Con la parabola (y-3)^2 = 6(x-5),Calcula su vertice,su foco y la directriz.
3.Halla las coordenadas del vertice y los focos de una parabola con ecuación
1.Con la parabola (x-3) ^2 = 8(y-2),Calcula su vertice,su foco y la directriz.
2.Halla las coordenadas del vertice y los focos de una parabola con ecuación
y^2 - 6y -8x + 17
3.Con la parabola (y-2)^2 = 8(x-3),Calcula su vertice,su foco y la directriz
4.Determina las coordenadas del centro,los focos,la excentricidad y los vertices de una hiperbola con ecuación 4x^2 - 3y^2 - 8x - 8 = 0
5.Determina las coordenadas del centro,los focos,la excentricidad y los vertices de una hiperbola con ecuación: y^2 - 2x^2 - 4x - 4y = 0
E J E R C I C I O S D E P R A C T I C A
1.Halla los vertices,los focos y las directrices de una parábola con ecuación:
y^2 - 4y - 6y + 9 = 0
2.Con la parabola (y-3)^2 = 6(x-5),Calcula su vertice,su foco y la directriz.
3.Halla las coordenadas del vertice y los focos de una parabola con ecuación
y^2 - 3y -4x + 13 = 0
4.Determina las coordenadas del centro,los focos,la excentricidad y los vertices de una hipérbola con ecuación 6x^2 - 5y^2 - 7x - 9 = 0
5.Determina las coordenadas del centro,los focos,la excentricidad y los vértices de una hiperbola con ecuación: y^2 - 4x^2 - 5x - 6y = 0